About Me
I am a theoretical physicist specializing in statistical physics. I completed my undergraduate
studies at École polytechnique (X2018) and at ENS Paris (ICFP, theoretical physics).
I then earned my PhD from Sorbonne Université under the supervision of Raphaël Voituriez and Olivier
Bénichou; here is my PhD manuscript.
I am currently a postdoctoral researcher at Collège de France, working with Jean-François Joanny on active matter and out-of-equilibrium physics.
Research Interests
My research focuses on the quantitative characterization of space exploration by random walks, a question that lies at the heart of a wide range of phenomena. These include how ants explore their environment by following pheromone trails, how cells migrate while actively remodeling their extracellular matrix, and how long-term memory effects can influence the collapse of a financial index after a prolonged rise.
I investigate this classic and central problem from a new perspective, with particular emphasis on the interplay between the geometry of the explored territory and the intrinsic memory of the walker’s past trajectory, the defining feature of non-Markovian walkers. Such behavior makes exploration properties particularly challenging to analyze; yet it is ubiquitous across science, appearing in contexts as diverse as physics, biology, and finance. As the late N. G. van Kampen famously said, non-Markovian dynamics are the rule rather than the exception in Nature.
Publications
.png)

J. B., L. Régnier, A. Barbier-Chebbah, O. Bénichou, R. Voituriez
Nature Communications (2025). Featured as a Scientific Result by CNRS Physique.
This article addresses a central limitation in the study of random explorations: in most real systems, the microscopic origin of memory is unknown or too complex to model, making it difficult to infer a reliable description of exploration dynamics. To overcome this difficulty, one must identify unifying principles governing how diverse random walks explore space, enabling model-free predictions. We introduce the flip, a purely geometric observable that quantifies the propensity of a process to reverse its direction of exploration—schematically, a forager turning back to exploit previously visited regions. We show that the flip probability follows a striking universal scaling law, decaying as \( A/n\), where \( n \) is the size of the visited territory, and \(A \) is a process-dependent constant, acting as a fingerprint of the type of memory. This framework applies across a wide class of models and is validated on both biological trajectories and financial time series, providing a robust, model-free tool to quantify exploration in systems with memory.
J. B.
Physical Review Letters (in press).
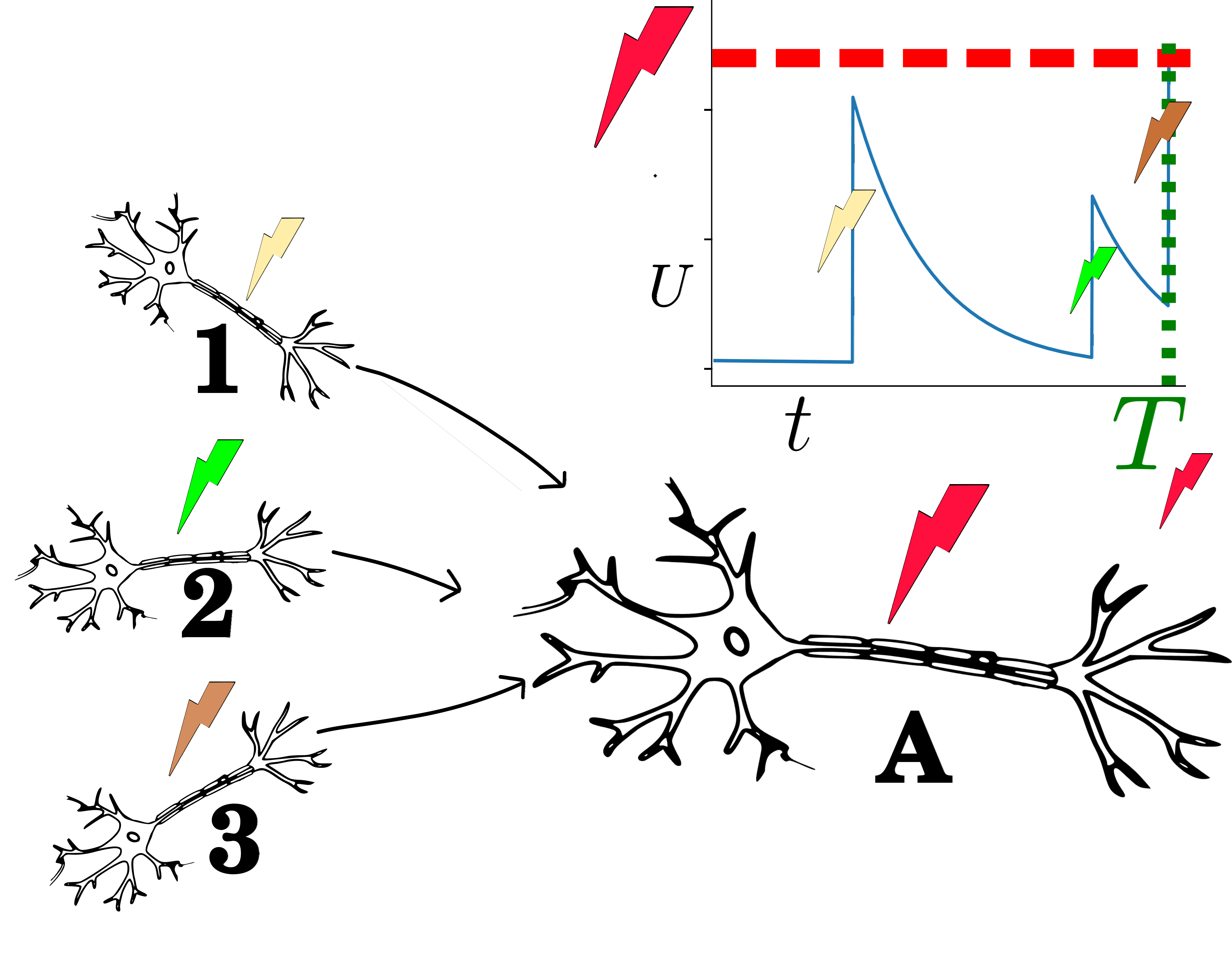
This paper derives the first general asymptotic expression for first-passage times of renewal shot-noise processes with non-Poisson statistics and impulsions of exponential amplitudes. It reveals how memory encoded in inter-arrival times modifies the classical Arrhenius law, with direct implications for neuronal firing, gene expression, and other excitation–relaxation systems exhibiting non-Markovian dynamics.
J. B., L. Régnier, O. Bénichou, R. Voituriez
Physical Review Letters 134, 197103 (2025)
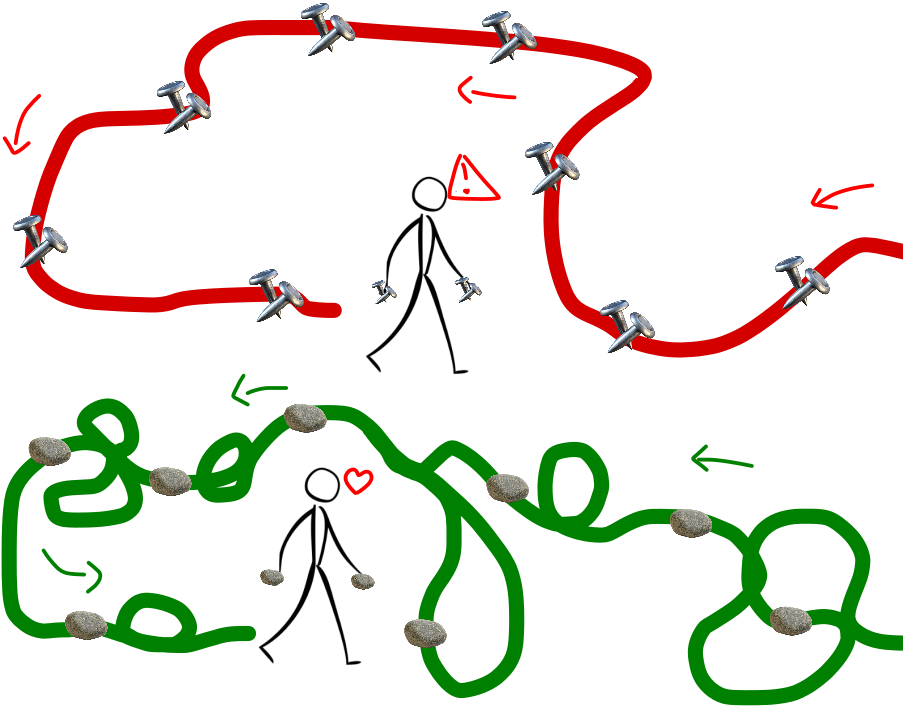
The persistence exponent \( \theta \) quantifies the long-time probability \( S(x,t) \propto t^{-1-\theta}\) that a random walker has never visited site \( x\). This is a central observable for characterizing exploration processes, with a long history in statistical physics. Self-interacting random walks provide a minimal and physically motivated class of non-Markovian models in which the walker continuously modifies, and responds to, its own past trajectory, a mechanism relevant to systems ranging from animal foraging to migrating cells and non-reversible MCMC algorithms. In this work, we obtain the first exact determination of persistence exponents for one-dimensional self-interacting random walks. By exploiting their hidden algebraic structure, rooted in Tóth’s Ray–Knight theorems, we provide quantitative tools to detect and characterize self-interaction–induced memory effects from experimental trajectories.
J. B., O. Bénichou, R. Voituriez
Physical Review Letters 133, 157101 (2024)
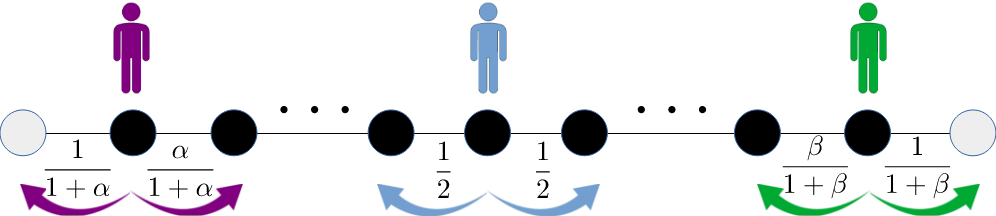
This work derives exact expressions for the propagator \(P(x,t)\), that is, the probability that the walker is on site \( x \) at time \(t \), for two central universality classes of one-dimensional self-interacting random walks: the polynomially self-repelling walk and the saturating self-interacting walk. These results provide access to fundamental observables that had remained analytically out of reach and reveal intrinsically non-Markovian mechanisms governing spatial exploration, including non-monotonic propagators induced by self-repulsion.
This paper has been put forward by Wolfram Research.
J. B., T. Jakuszeit, O. Bénichou, R. Voituriez
Physical Review E 110, 014604 (2024)
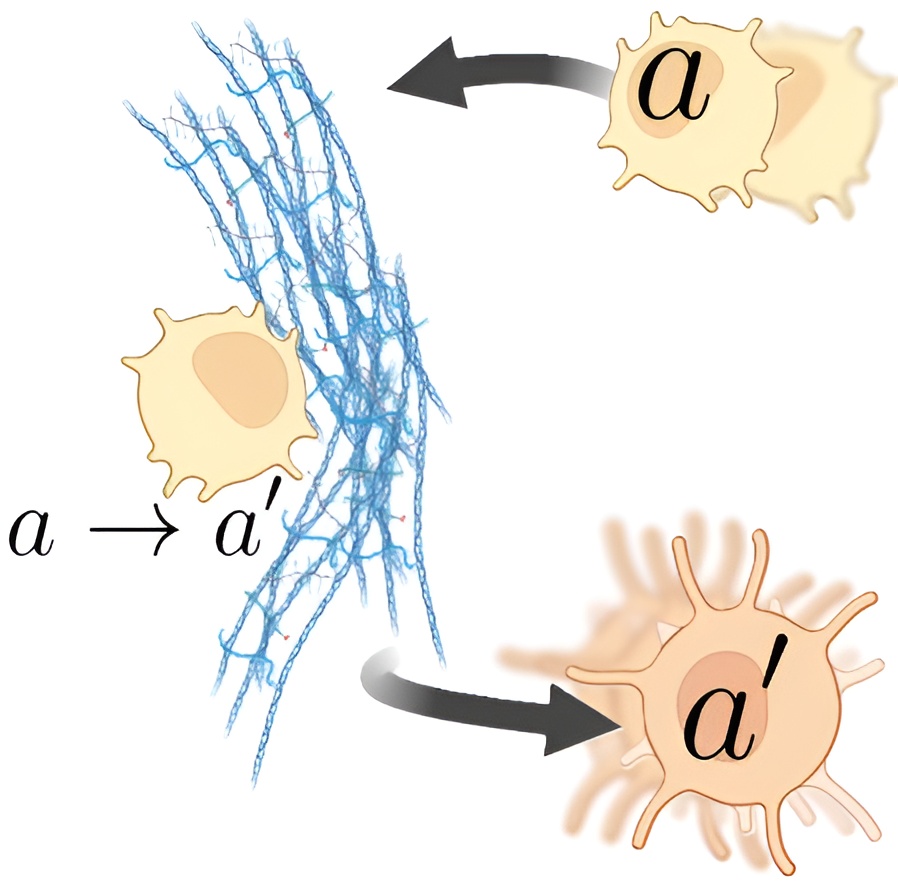
This article introduces a general analytical framework for locally activated random walks, motivated by biological systems in which cells adapt their motility after traversing specific regions of their environment. In particular, it models situations where cells such as dendritic cells modify their speed or persistence after passing through confined or chemically rich zones. The theory shows how such local activation mechanisms generate strong memory effects, including aging, dynamical trapping, and non-Gaussian exploration in arbitrary dimensions, and identifies robust signatures that can be directly tested in cell migration experiments.
